循環小数のフシギ

エクセルで２のｎ乗の表を作ってたら
循環小数って言うのに出会った

いろいろ調べてみたら面白いぢゃんか

循環小数

循環小数とは、

0.111111111・・・・・・
0.101010101・・・・・・
0.125125125・・・・・・

のように少数点以下のいくつかの数字が無限に繰り返される少数のこと
これらは全て分数で表示することができるんだって！

コウフンスルネー!



＊循環小数になる分数の作り方

分数の作り方は、循環する部分の数字を分子に、それと分子と同じ桁数の9を分母にした分数を作ればいいんだって！
かんたんねー

そんなわけで上の循環小数は、それぞれ次のような分数になります

0.111111111・・・・・・　⇒　1／9
0.101010101・・・・・・　⇒　10／99
0.125125125・・・・・・　⇒　125／999


それでは、　0.999999・・・・・・　という循環小数はあると思いますか？

答えは、「ある」ような・・・・・・、「ない」ような・・・・・・、
0.99999・・・・・・の場合は
上記に当てはめて分数をつくってみると
分子は9が繰り返されているので、９
分母は分子と同じ桁数の9を分母にすればいいんだから、９

0.99999・・・・・・=9/9＝１

となりますなー
これはイコールなんだろうかね?

0.99999って数字はないってこと？あるってこと？
おしえてください


＊0.99999・・・・・の作り方


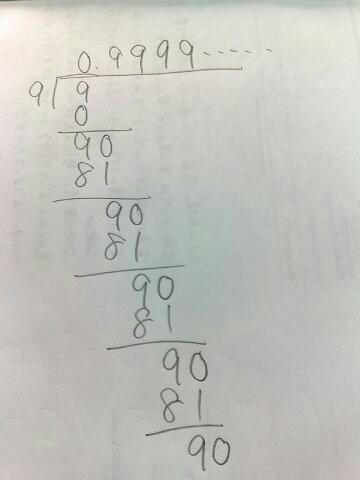
9÷9の割り算で最初に1をたてずに次の位で9とすると、0.99999・・・・・・という循環小数が出来上がります
ちょっとずるいようなー

8÷8でも7÷7でも結果は同じですな

果てしなく1に近いって事で納得しましょうか







横道にそれますが
1÷3はなんでんしょ？
1/3？
0.3333333?

1÷3=1/3とすると
1÷3×3=１になりますね

1÷3=0.3333333........とすると
1÷3×3=0.9999999......になりますね

分数で計算するとちゃんと1になるけど
小数で計算すると0.99999......になるんですね

ちゃんとがどうちゃんとかはわかりませんけど

フシギぢゃない?
ドキドキしない?
びりびりしない?



＊シンプルな分数の循環小数

5／7という分数も循環小数（0.714285714285・・・・・）になりますが、この分数も循環小数の作り方にあてはまります。（⇒714285／999999）

この分数には分子・分母共通に142857（＝3×3×3×11×13×37）という約数が存在するので、分子および分母をこの約数で割ると5／7になります。

714285／999999　⇒　714285÷142857／999999÷142857＝5／7

興味のある方は、電卓のキーをたたいてみてください

たのしいよーー！